
Marty Supreme, Ramble Little
I had been excited for Marty Supreme for over a month before I finally saw the movie. It all started with this dumb viral zoom skit. Digging further into advance screening sentiments, I had a biased prior belief that this movie, capitalized as Dream Big, was way darker than it was commercially sold as; that this was beyond American dream, maybe about some money-hungry sociopath who’s chasing their aims at the cost of sacrificing and scamming their close ones, much like the whiplash plot in spirit, or uncut gems.

Stochastic Vol and Heston Model
So it was not until 2025 that I developed some genuine interests in quant finance. I briefly had some reading in 2023/2024 but I always stopped at “oh, here goes the Itô’s lemma; there goes Feyman-Kac; Markowitz mean-variance formulation seems familar”, never really dived into exotics and exchange rates, the real stuff people are playing around. Well, now since I really want a job, I need some practitioner’s guide and I find it fascinating.

Blackwell Approachability
Pretty much all the work I did these years are related to learning in games. And one of the most important theorem that pulled me into this is Blackwell’s Approachability theorem 1 (truth is I never really did anything on it because it does not imply much on computation). This theorem connects geometry, game theory, and the very essence of no-regret learning. Regarding this concept, my belief used to be that approachability implies the existence of no-regret algorithms. Turns out the connection is much stronger: the two are, in a very strong sense, algorithmically equivalent.

Reinforcement Learning with Human Feedback
I would love to think of the ICML 2023 conference in Honolulu as a pivotal event for my P.h.D. research. During that time I was kind of talking to Reagan and having the time of my life. I remember in the conference there was a workshop session named sampling over discrete space. It felt serendipitous, like the universe was pointing me toward somewhere significant, much like how my brilliant colleague Tao pointing to the bright future here haha

Bayesian Holonic (Global) Games
This past year I suffered a lot mentally and financially, my funding got paused and my girlfriend Sam (check out her spotify!) lost her boojee A.P.C. job. So I haven’t posted for a while. It’s really a leisure and effort to write stuff consistently (because wtf am I supposed to write?!!?). But the coding agents (Claude, Gemini etc..) really revolutionarized my efficiency, and shamelessly I have to admit that I use them a lot to “vibe code” and even do research, with sufficient human surveillance. So hopefully, I will resume writing for my own sanity.

About Me
When you write an About Me, you want something permanent. Well, I go by ‘Union’ — a homophone of my Chinese name (禹年) that I find neat and hope will stick. What won’t last much longer is that I’m finishing my PhD at NYU Tandon, and here goes the elevator pitch for my research:
I develop algorithms that optimize the transient processes of multi-agent decision-making in complex systems, leveraging game theory and machine learning across domains like communication, transportation, and finance.

What (on earth) is a Sufficient Statistic?
It certainly bothered me (not any more) to hear people casually dropping the word “sufficient statistics” in their talks, often describing some of their ‘‘observations’’ or ‘‘samples’’ that they feel like are ‘‘sufficient’’ for them to make certain decisions. The thing is, the word ‘‘sufficient’’ comes with a very rigorous definition, that may not even hold in those frameworks. For example, a lot of traffic control algorithms use measured vehicle streamed data to learn some embeddings as the input, the downstream tasks could be variable speed limit for certain highway segments for example, and people might call the embeddings ‘‘sufficient statistics’’. Umm, … truth is I don’t even where to start with this.

The Lorenz dynamics and Butterfly Effect
Chaotic behavior can emerge even in simple dynamics such as replicator, and Rock-Paper-Scissor oscillators, depending on the game settings. To begin with, we first define what is chaos qualitatively: “Chaos can be described as long term, aperiodic behaviour that exhibits sensitive dependence on initial conditions. Sensitive dependence on initial conditions implies that nearby trajectories diverge exponentially fast over time.” Or, by Edward Lorenz, when the present determines the future but the approximate present does not approximately determine the future.

Talagrand's Isoperimetry inequality
This post is in celebration of Michel Talagrand winning Abel prize. Not to overly romanticize this but this is pretty much a come back story because back in the days of last century, “The type of mathematics I do was not fashionable at all when I started. It was considered inferior mathematics.” –Michel Talagrand.
Now we’ve seen significance of his contribution to the concentration of measure, suprema of stochastic processes and spin glass, all partially owing to his celebrated isoperimetry inequality in product probability space. What is an isoperimetry inequality? It is a concept in mathematics, particularly in the field of geometry and geometric analysis, that compares the length (or perimeter) of a closed curve to the area of the region it encloses, establishing that among all shapes with the same perimeter, the circle has the maximum area. For example: $$ 4 \pi A \leq L^2 $$ where the equality holds if.f. the curve is a circle. In a more general sense, the isoperimetric inequality relates the volume of an $n$-dimensional domain to the surface area of its boundary, with the sphere in $n$-dimensional space providing the optimal (maximum volume for a given surface area) ratio. Applying this concept to probability space, Talagrand was able to prove the following:
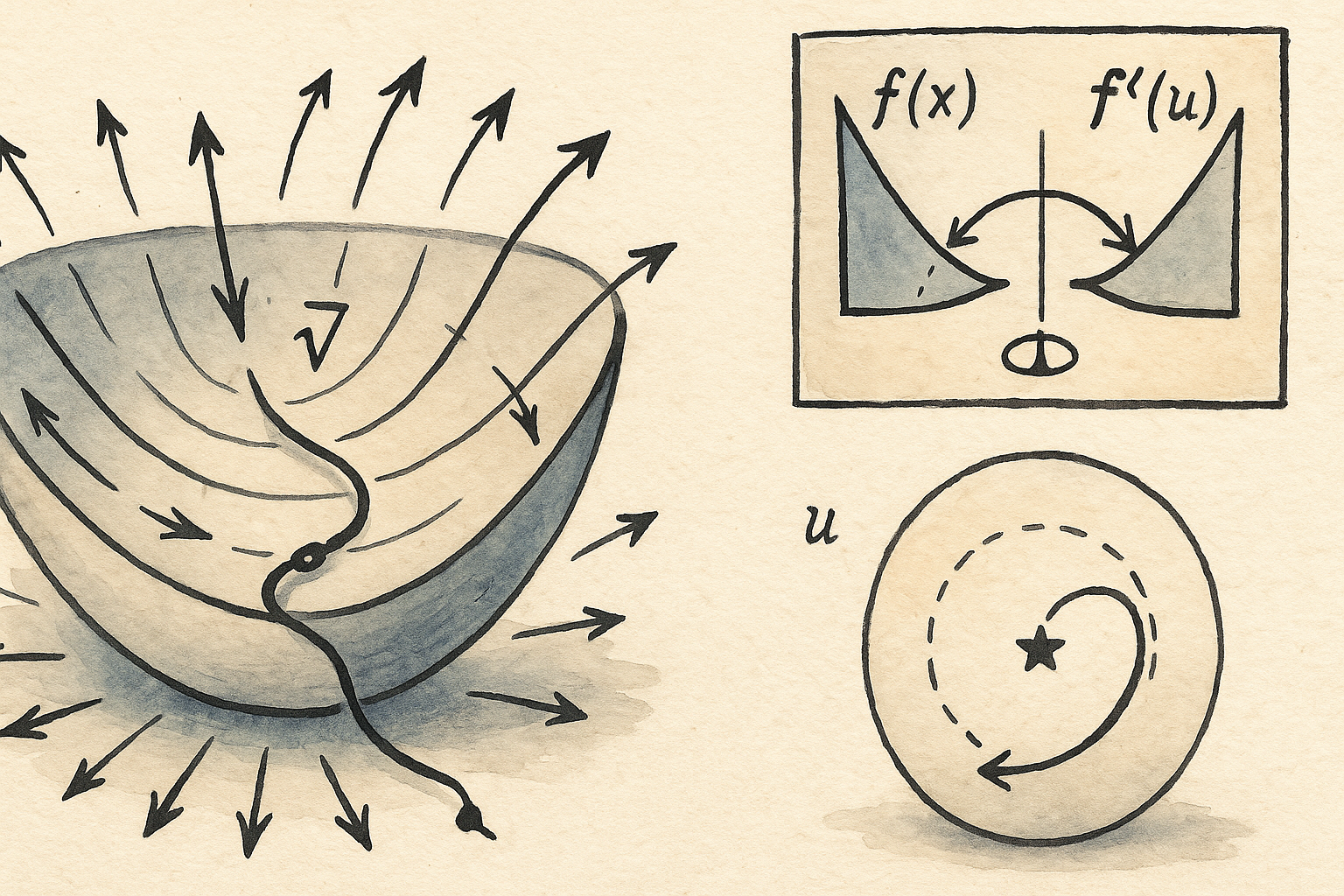
A Variational Perspective On Gradient Descent
In this post I just want to share a simple and elegant idea from a Control System Letter paper written by Maxim Raginsky et al.1. This idea largely inspired my recent work on multi-agent learning in (monotone) games2, which I might devote another post to talk about if I happen to get some interesting results out of it.
The idea starts from here: we all know that the archetype of solving convex optimization problem is through gradient descent: $$ x_{k+1} = x_k - \nabla f(x_k), $$ which, in continuous time, corresponds to an autonomous dynamical system: $$ \dot{x} = - \nabla f (x) , \quad x(0) = x_0. $$ A natural question to ask is what are the hidden objectives being achieved along the gradient flow. This question was approached in a “inverse optimal control” fashion, i.e., given an autonomous dynamical system, identify the close-loop control and its corresponding optimal control problem. In this approach, the Fenchel-Young inequality played a crucial role to formulate the optimal control problem, as was extensively used in the variational principles introduced by Brezis and Ekeland3.

Some Notes on Dueling Bandits
The dueling bandit problem natrually fits the description of a variety of recommendation systems that require ‘’learning on the fly’’, yet have no explicit access to a ‘‘reward’’ model. Instead, the ‘‘human’’ feedback part takes the form of ‘‘choices’’, ‘‘votes’’, or some discrete forms. Hence, oftentimes a learning protocol proceeds at time steps \(t = 1, \ldots, T\):
- The algorithm chooses a pair of arms \( a_i, a_j \) from \(K\) available ones;
- The oracle/human feedback/nature reveals the winner arm \( a_i \), with probability \( P(a_i \succ a_j)\), \( P(a_i \prec a_j) = 1 - P(a_i \succ a_j) \)
So the feedback is either \(a_i\) or \( a_j \), the preferences forms a matrix \(P \in \mathbb{R}^{K \times K}\) such that \( P + P^{\top} = I\) which defines the hidden information of the dueling bandit problem. The cumulative regret in the stochastic dueling bandit setting is: $$ \mathcal{R}_T = \sum_{t=1}^T P( a^* \succ a^t_i ) + P( a^* \succ a^t_j ) $$ where \(a^* \) is usually the Condorcet winner, i.e., \( P( a^* \succ a_j) > \frac{1}{2} \ \ \forall j \in [K], a_j \neq a^*\). Condorcet winner is a pretty straightforward idea, which might not exist in general cases. To see that, suppose there are three candidates: A, B, and C, and three voters with the following preferences:

Erdos-Szekeres Theorem
This post is dedicated to Erdos-Szekeres Theorem, which says:
ES Thm. (Monotone sequence)
For any positive integer $n$, any sequence of $n^2 + 1$ distinct real numbers contains a monotone subsequence of length at least $n+1$.
This means that within any sufficiently long sequence, there is either an increasing subsequence or a decreasing subsequence of a certain minimum length.
There’s another version of the theorem statement coming from the 1935 paper by Paul Erdos and George Szekeres1, which concerns combinatorial geometry. It says:
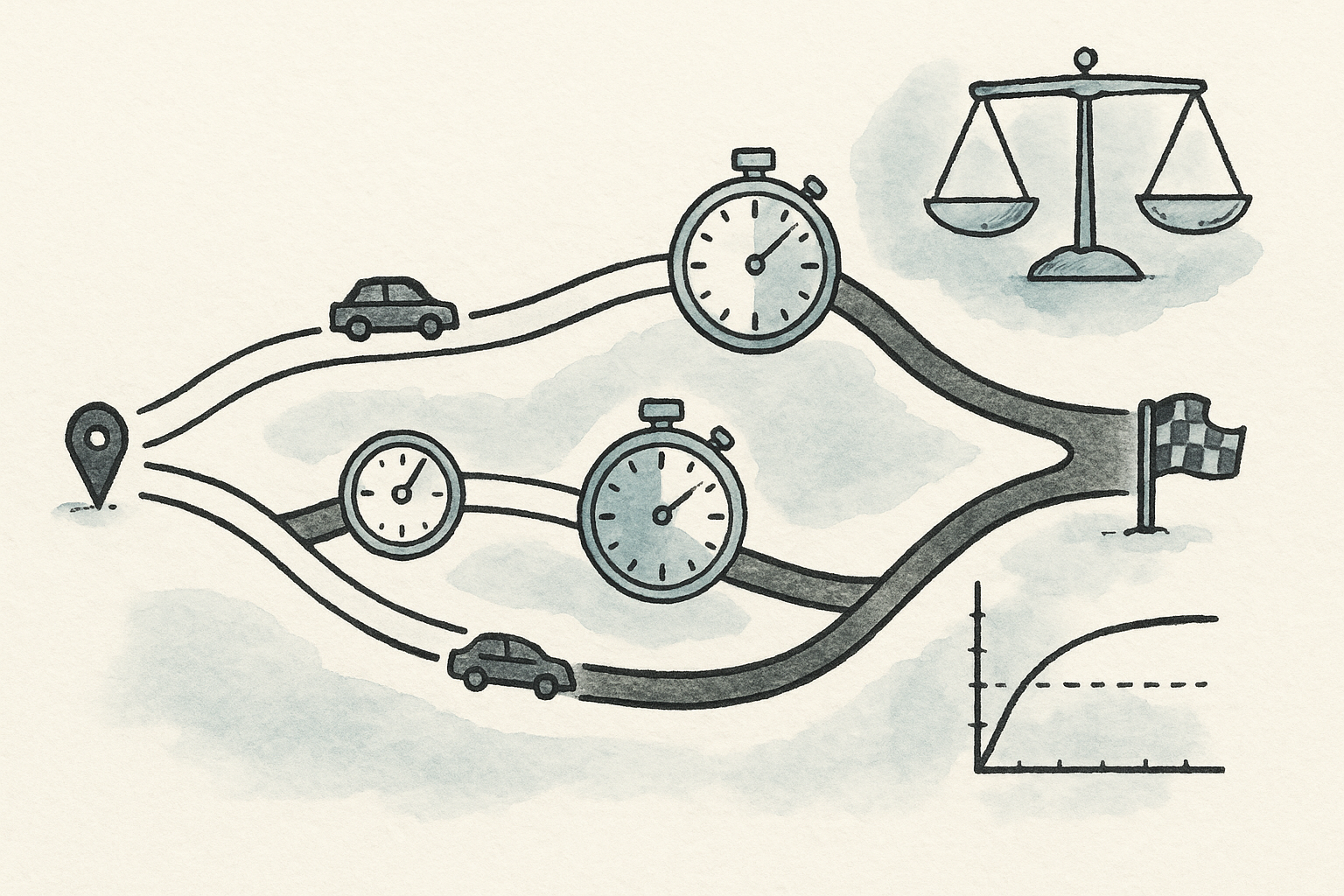
Wardrop Equilibrium
I remember having those unpleasant lines in our high school canteen, flooded by the starving students queeing for their lunch, I would always pick a window with fewer people waiting, compromising myself with awful food.
Another similar thought that always stricked me was the odds that tourists always pick the same time to travel, there’s almost always traffic congestion everywhere during holiday seasons. Yeah, lives have been always so hard.
On the first level of thinking, when there’s a lack of resource you attempt to find alternatives, e.g., picking another time for traveling, another food window, etc.. The level two thinking is maybe ‘‘since other people are avoiding holidays, what if I insist on going out on holidays’’? Or maybe there’s a twisted level three thinking, ‘‘what if everybody thinks like the level two thinker, ….’’ It’s somewhat intimidating to follow this infinite hierachy, but definitely rewarding, as there are certainly moments when people are regretting their travel decisions, thinking to themselves ‘‘I probably should not have gone the high way.’’

Nesterov
I did a presentation in a group meeting to briefly review the lower complexity bound of first-order convex optimization; and how Nesterov proceed to match the lower bound using the estimation sequence, the slides are here.
Consider an unconstrained optimization problem: $$ \min_{x \in \mathbb{R}^n} f(x) . $$ Here, \(f \in \mathcal{C}^1\) is a convex, $L$-Lipschitz smooth function. Obviously we can solve this problem by using first-order methods, using iterations:
$$ x_{k} \in x_{0} + \operatorname{Span} \left \{f^{\prime} \left (x_{0} \right ), \ldots, f^{\prime} \left (x_{k-1} \right )\right \}. $$

Monge Partition
There are many service centers in our city, such as MTA subway station, Vaccination sites, Wifi hot-spots, Blue Bicycles, hospitals, parking lots etc.. Meanwhile, there are so many people in need of these services who are distributed maybe according to some point processes. The question of how to efficiently make assignments between the demands and the service centers gives rise to a special type of problems called semi-discrete optimal transport.
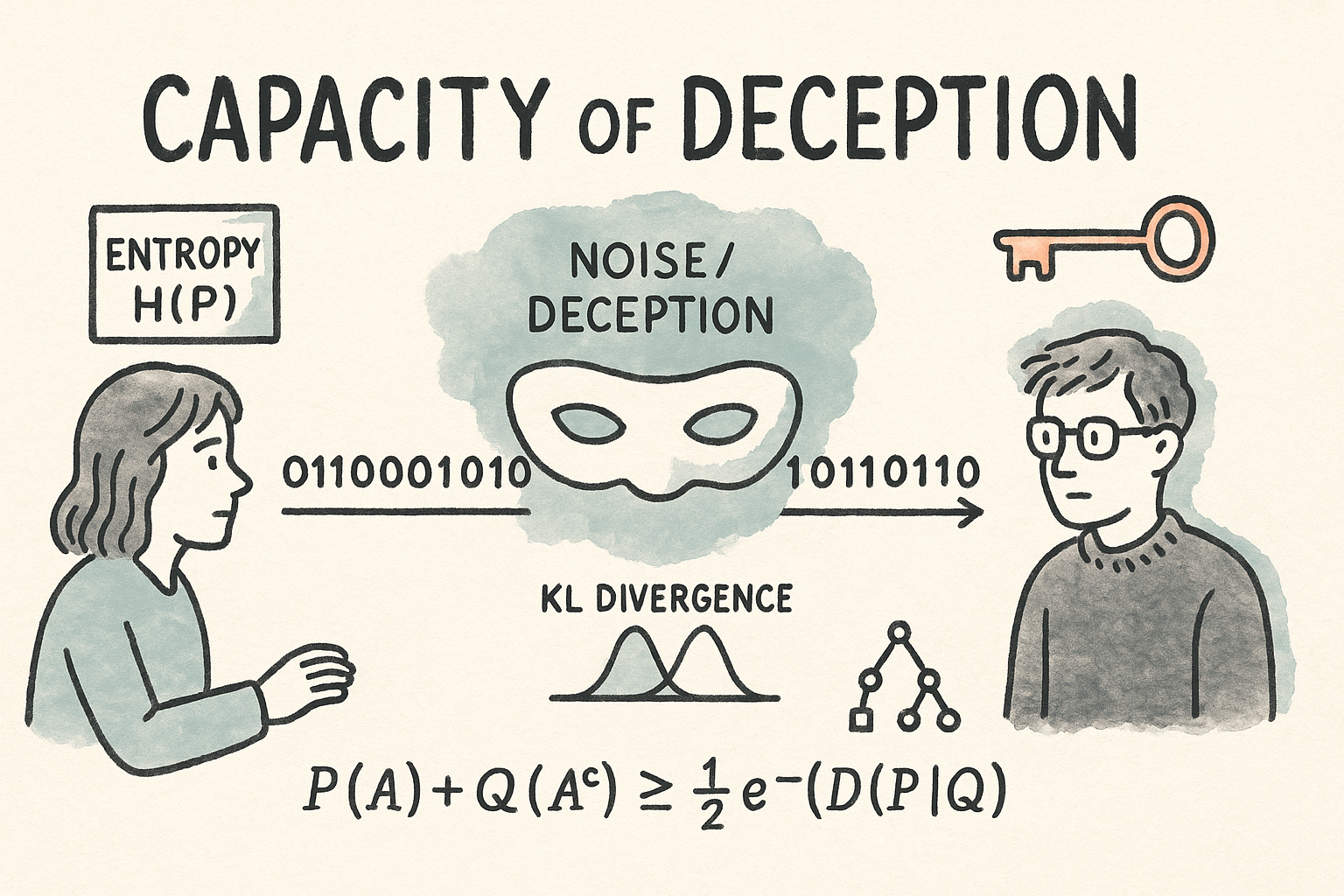
Capacity of Deception
This is pretty much scribed from Tor Lattimore’s Bandit Algorithms book,Bandit Algorithms. This book has been the most informational item for me in a while. There is a chapter about the foundations of information theory, which is simply entropy, but the story telling reminds me of deception. Entropy, in plain words, is the measure of uncertainty for certain information; to communicate is to eliminate such uncertainty, to deceive, however, is to obscure certain information, hence to enforce such uncertainty. The duality has never been formalized as far as I know, because if you simply name the Shannon limit as the capacity of deception, you are doing anything innovative. But, if you think from Shannon’s perspective, wasn’t he also just doing the same thing? (Sorry for quoting my advisor here.) Anyway here goes the story: