
What (on earth) is a Sufficient Statistic?
It certainly bothered me (not any more) to hear people casually dropping the word “sufficient statistics” in their talks, often describing some of their ‘‘observations’’ or ‘‘samples’’ that they feel like are ‘‘sufficient’’ for them to make certain decisions. The thing is, the word ‘‘sufficient’’ comes with a very rigorous definition, that may not even hold in those frameworks. For example, a lot of traffic control algorithms use measured vehicle streamed data to learn some embeddings as the input, the downstream tasks could be variable speed limit for certain highway segments for example, and people might call the embeddings ‘‘sufficient statistics’’. Umm, … truth is I don’t even where to start with this.

The Lorenz dynamics and Butterfly Effect
Chaotic behavior can emerge even in simple dynamics such as replicator, and Rock-Paper-Scissor oscillators, depending on the game settings. To begin with, we first define what is chaos qualitatively: “Chaos can be described as long term, aperiodic behaviour that exhibits sensitive dependence on initial conditions. Sensitive dependence on initial conditions implies that nearby trajectories diverge exponentially fast over time.” Or, by Edward Lorenz, when the present determines the future but the approximate present does not approximately determine the future.

Talagrand's Isoperimetry inequality
This post is in celebration of Michel Talagrand winning Abel prize. Not to overly romanticize this but this is pretty much a come back story because back in the days of last century, “The type of mathematics I do was not fashionable at all when I started. It was considered inferior mathematics.” –Michel Talagrand.
Now we’ve seen significance of his contribution to the concentration of measure, suprema of stochastic processes and spin glass, all partially owing to his celebrated isoperimetry inequality in product probability space. What is an isoperimetry inequality? It is a concept in mathematics, particularly in the field of geometry and geometric analysis, that compares the length (or perimeter) of a closed curve to the area of the region it encloses, establishing that among all shapes with the same perimeter, the circle has the maximum area. For example: $$ 4 \pi A \leq L^2 $$ where the equality holds if.f. the curve is a circle. In a more general sense, the isoperimetric inequality relates the volume of an $n$-dimensional domain to the surface area of its boundary, with the sphere in $n$-dimensional space providing the optimal (maximum volume for a given surface area) ratio. Applying this concept to probability space, Talagrand was able to prove the following:
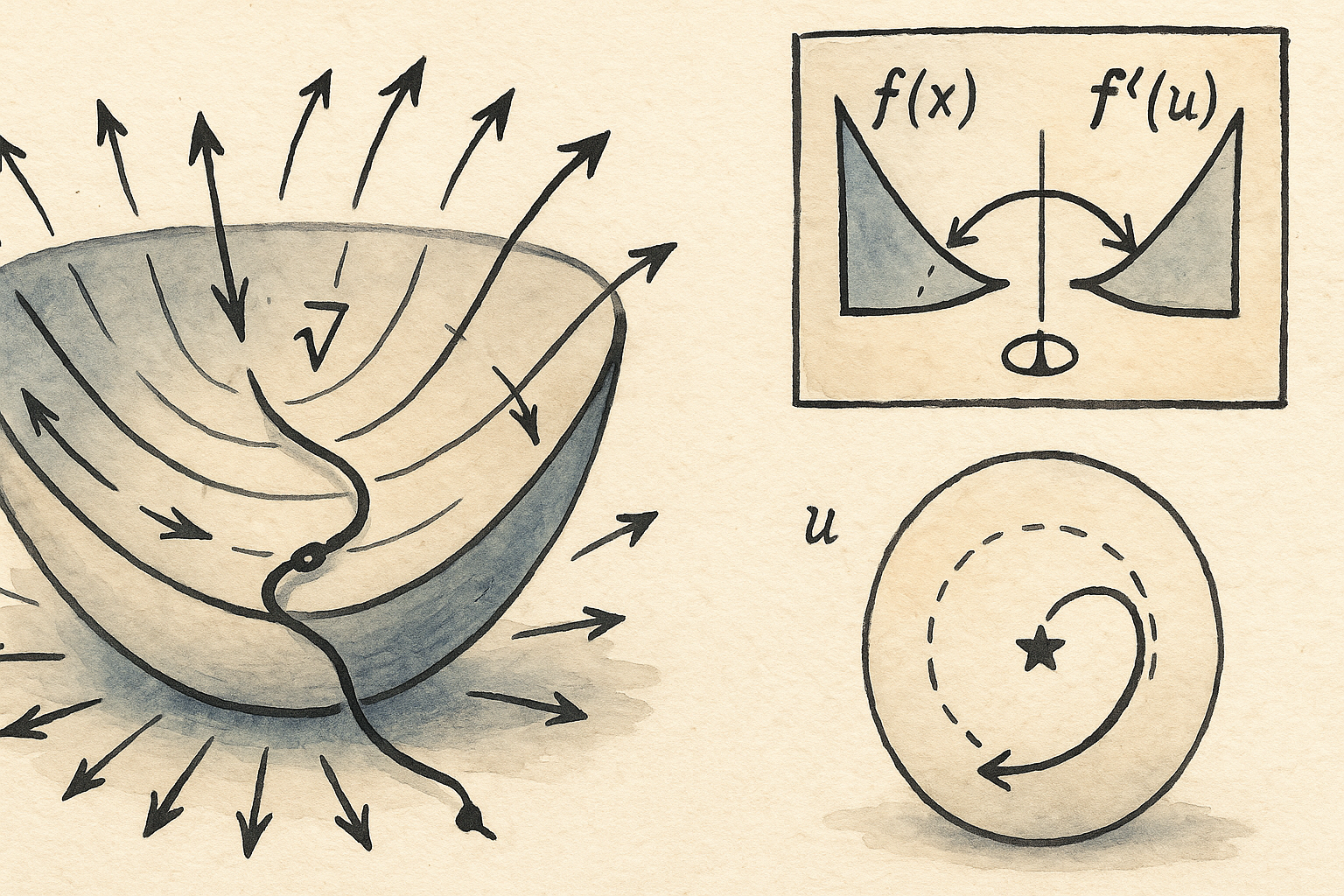
A Variational Perspective On Gradient Descent
In this post I just want to share a simple and elegant idea from a Control System Letter paper written by Maxim Raginsky et al.1. This idea largely inspired my recent work on multi-agent learning in (monotone) games2, which I might devote another post to talk about if I happen to get some interesting results out of it.
The idea starts from here: we all know that the archetype of solving convex optimization problem is through gradient descent: $$ x_{k+1} = x_k - \nabla f(x_k), $$ which, in continuous time, corresponds to an autonomous dynamical system: $$ \dot{x} = - \nabla f (x) , \quad x(0) = x_0. $$ A natural question to ask is what are the hidden objectives being achieved along the gradient flow. This question was approached in a “inverse optimal control” fashion, i.e., given an autonomous dynamical system, identify the close-loop control and its corresponding optimal control problem. In this approach, the Fenchel-Young inequality played a crucial role to formulate the optimal control problem, as was extensively used in the variational principles introduced by Brezis and Ekeland3.