Bayesian Holonic (Global) Games

This past year I suffered a lot mentally and financially, my funding got paused and my girlfriend Sam (check out her spotify!) lost her boojee A.P.C. job. So I haven’t posted for a while. It’s really a leisure and effort to write stuff consistently (because wtf am I supposed to write?!!?). But the coding agents (Claude, Gemini etc..) really revolutionarized my efficiency, and shamelessly I have to admit that I use them a lot to “vibe code” and even do research, with sufficient human surveillance. So hopefully, I will resume writing for my own sanity.

So I am a huge hypocrite–throughout the years I’ve witnessed tons of people rebranding existing/trivial phenomenon/methodologies as ‘’novel frameworks’’. I mean, aren’t we all? Even Shannon was just applying probability theory, except for it actually opened the pandora box. To some degree I believe being completely innovative is inherently impossible as you’ve gotta find some shoulders to stand on. It gets harder when you’re under constant pressure to publish, get grants, and do rebuttal with reviewers who might be having a bad day.

Sometimes I wonder where the objective bar, for what counts as “innovative enough”, actually is. The sheer volume of academic papers flood into the system, how much values do they actually create? Overworked reviewers delegate to grad students or (God help us) undergrads, are they able to catch when the emperor has no clothes?

“Holonic Risk”

This is the paper my advisor has been writing. He gradually accustomed himself with ChatGPT that it just infiltrated to his everyday editing of stuff (the Overleaf history and code style shows it all,) which I can’t say if it’s good or bad. The core idea is that he envisioned this networked chunks of players that interact with each other through a set of specifically structured utility functions. A “holons” is a “chunk of players”, and the Nash equilibrium, as you may upgrade it into Bayesian, is a “Holonic equilibrium”.

Here’s a global game¹ example “holonic Bayesian game”:

Players: Set of voters $N = \bigcup_{i \in I} N_i$ where $I$ indexes committees (holons) and $N_i$ are voters in committee $i$.

Types: Each voter $k \in N_i$ has private type $\xi_k^i \in \{0,1\}$ drawn from Bernoulli$(p)$, representing their preference strength.

Actions: Binary voting decision $x_k^i \in \{0,1\}$.

Information Structure: Each voter observes only their own type $\xi_k^i$ but knows the type Bernoulli distribution $p$ is common across all voters.

Payoff Structure: For voter $k$ in committee $i$, the utility function is: $$ U_k^i(x_k^i, x_{-k}^i, \omega_{-i}; \xi_k^i) = \mathbf{1}_{{ \omega^i = 0}}(c_0 + c_1 x_k^i) + \mathbf{1}_{ { \omega^i = 1 } } c_2 \cdot \mathbf{1}_{ { x_k^i \neq \xi_k^i }} $$

where $\omega^i \in {0,1}$ is the committee outcome and $\omega_{-i}$ represents other committees’ outcomes.

The “holonic” aspect reduces to this coupling mechanism:

$$ \omega^i = \mathbf{1}_{\left\{ \sum_{k \in N_i} x_k^i \geq \theta + \gamma \sum_{j \neq i} \omega^{j}\right\}}$$

So committee $i$ succeeds if its vote total exceeds a threshold that increases linearly with the number of failed external committees. The parameter $\gamma \geq 0$ controls coupling strength.

To be fair this cannot be counted as completely a global game because it has atomic players. But the common feature is that you can sort of leverage the global symmetry to analyze the Nash equilibrium.

Bayesian Equilibrium Analysis

In a Bayesian Nash equilibrium, each voter chooses a strategy $\sigma_k^i: \{0,1} \rightarrow \{0,1\}$ that maximizes expected utility given their beliefs about others’ strategies and external outcomes.

Equilibrium condition: For truth-telling to be a Bayesian Nash equilibrium, we need basically: $$ \mathbb{E}[U_k^i(\sigma^i_k(\xi_k^i), \sigma_{-k}^i(\xi_{-k}^i), \omega_{-i}; \xi_k^i)] \geq \mathbb{E}[U_k^i(1- \sigma^i_k(\xi_k^i), \sigma_{-k}^i(\xi_{-k}^i), \omega_{-i}; \xi_k^i)] $$ for all $k, i$ and both values of $\xi_k^i$. So, you have $|\mathcal{I}|$ times $n$ set of equations for three types of strategies:

Truth-telling strategy: $\sigma_k^i(\xi_k^i) = \xi_k^i$ (vote your type).

Truth-reversing strategy: $\sigma_k^i(\xi_k^i) = 1 - \xi_k^i$ (vote against your type).

Pooling strategies: $\sigma^i_k(\xi_k^i) = 1$ or $\sigma^i_k(\xi_k^i) = 0$ (vote constantly).

For truth-telling strategy, the equilibrium condition reduces to the incentive compatibility constraint: $$\mathbb{P}(\omega^i = 1) \geq \frac{c_1}{c_1 + c_2}.$$ That is to say, under the strategy, I calculate the success probability within one holon $i$, it has to be above certain threshold for this strategy to be ``okay’’ as an equilibrium, but to calculate the success rate under a type prior, you have to consider other holons as well, this eventaully becomes a tangled ‘‘chicken-egg’’ problem.

The Fixed-Point Problem

Most ‘‘chicken-egg’’ problem can be solved by fixed-point equations. Under symmetric truth-telling strategies, all committees have the same success probability $q$. The number of external failures follows $\text{Binomial}(|I|-1, 1-q)$, leading to the fixed-point equation:

$$q = \sum_{z=0}^{|I|-1} \binom{|I|-1}{z} (1-q)^z q^{|I|-1-z} \cdot \mathbb{P}\left(\text{Binomial}(n,p) \geq \theta + \gamma z\right)$$

For large $n \to \infty$, using the normal approximation: $$q = \sum_{z=0}^{|I|-1} \binom{|I|-1}{z} (1-q)^z q^{|I|-1-z} \cdot \Phi\left(\frac{np - \theta - \gamma z}{\sqrt{np(1-p)}}\right)$$

In the limit $|I| \rightarrow \infty$ with $\delta = \gamma |I|$ fixed, this becomes: $$q = \Phi\left(\frac{np - \theta - \delta(1-q)}{\sqrt{np(1-p)}}\right)$$

Existence and Uniqueness of Equilibria

Since there is no other way around than enumerating if every possible strategy satisfies the incentive compatibility, the key mathematical questions become:

1. Existence: When does a solution $q^* \in [0,1]$ exist?
2. Uniqueness: When is the solution unique?
3. Stability: When are equilibria robust to perturbations?

Uniqueness condition: The mapping $T(q) = \Phi\left(\frac{np - \theta - \delta(1-q)}{\sqrt{np(1-p)}}\right)$ is a contraction when: $$\frac{\delta \phi\left(\frac{np - \theta - \delta(1-q)}{\sqrt{np(1-p)}}\right)}{\sqrt{np(1-p)}} < 1$$

where $\phi$ is the standard normal density. This is guaranteed when $\delta$ is sufficiently small relative to $\sqrt{np(1-p)}$.

Multiple equilibria: For large $\delta$, the system can exhibit bistability with equilibria near $q = 0$ and $q = 1$, separated by an unstable interior equilibrium. So the interpretation is, the more coupling between holons, the more chaotic it becomes. Below is kind of a relationship between $q$ and the prior $p$, the theoretical plot got twisted because at some of the $p$ the fixed point equations can’t be solved.

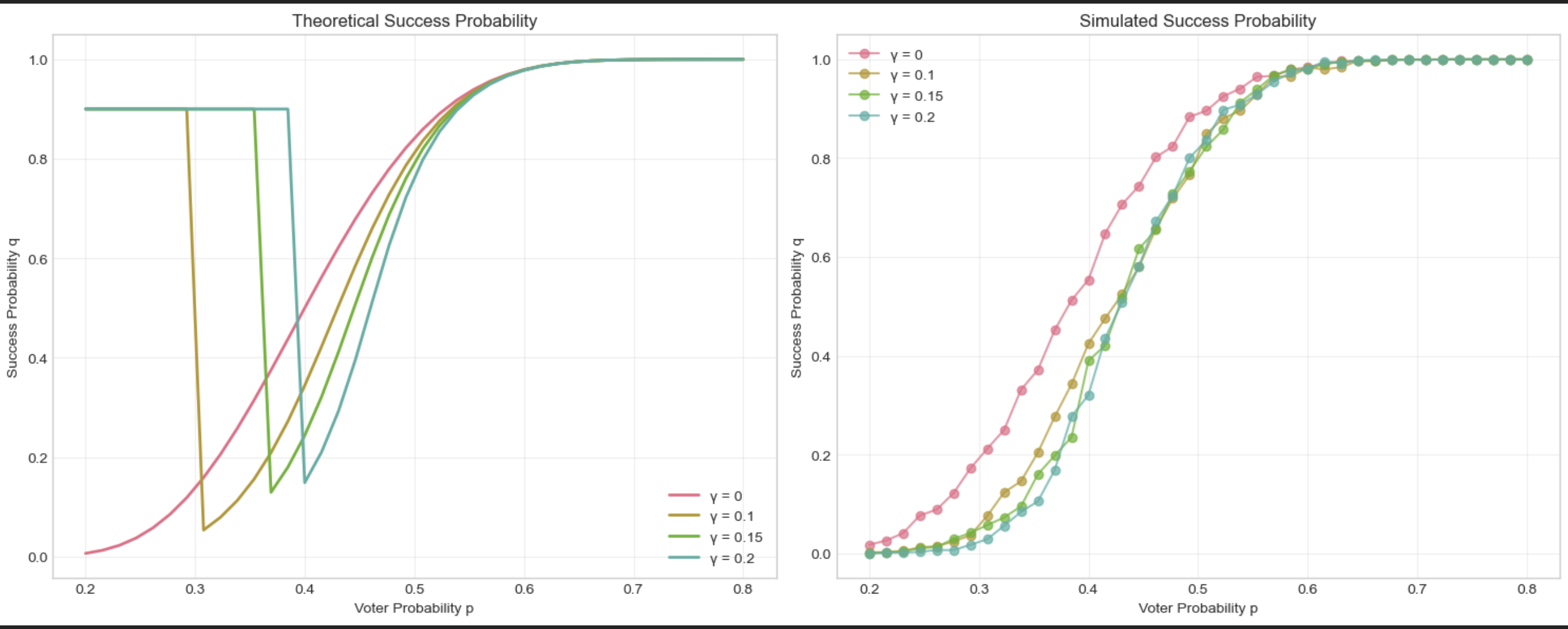
With a simple set up like this it’s already not very computationally convenient for seeking the equilibrium, so you can imagine how hard it is for general Bayesian Nash equilibrium.

The motivation of coming up with a system like this is still something I couldn’t figure out, because what do I know. But we should call it what it is. LOL.